The Information Theory Edition

On ideas, predictability, and understanding the world

Noah here. The best ideas burrow their way into your brain and never come out. For me at least, the concepts that come to mind—like McLuhan’s “medium is the message”—are impressive in the simplicity and breadth of application. The ones that burrow deepest also often contain some counterintuitive core: they don’t necessarily match our innate understanding. For McLuhan that was about the natural inclination to focus on the content, not the delivery medium. Of course, he realized this and called it out. “The ‘content’ of a medium,” McLuhan wrote in Understanding Media, “is like the juicy piece of meat carried by the burglar to distract the watchdog of the mind.”

Information theory is another one of those ideas for me. I only learned about it in the last few years thanks to this excellent Aeon piece by Rob Goodman and Jimmy Soni . It’s the brainchild of the mathemetician Claude Shannon, who developed the first technical definition for information in his famous paper “A Mathematical Theory of Communications.” The gist of Shannon’s idea is that information is actually a measure of uncertainty. If you ask someone to tell you what 2+2 is equal to, their answer will carry far less information than if you ask for what inspires them. Shannon proved that mathematically, showing that you could measure uncertainty in something he called bits. The more uncertain, the more bits. When you compress a photo of the sky, for instance, you’re in part lowering its uncertainty by removing some of the many shades of blue that actually exist. 

Why is this interesting? 

While Shannon’s idea is amazing in its own right, the explanation he offers in his famous paper is equally impressive. At the base of the whole thing is a recognition that information is probabilistic—we use certain letters and words more than others, for instance. Here’s my best attempt to take you through his logic (which some extra explanation from me).

Let’s start by thinking about English for a second. If we wanted to create a list of random letters we could put the numbers 1-27 in a hat (alphabet + space) and pick out numbers one by one and then write down their letter equivalent. When Shannon did this he got:

XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD

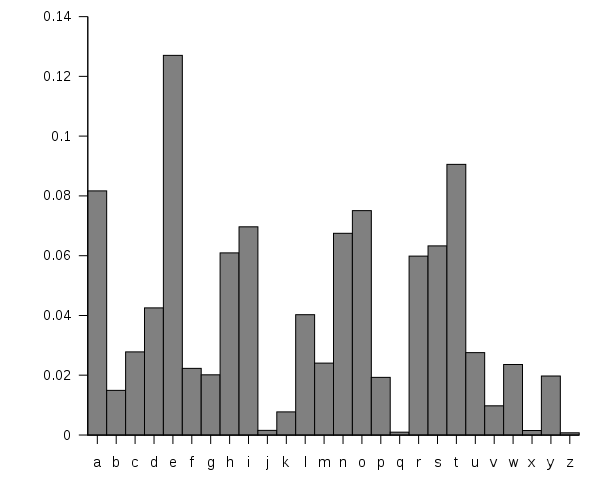
But letters aren’t random at all. If you open a book up and counted all the letters you wouldn’t find 26 letters each occurring 3.8% of the time. On the contrary, letters occur probabilistically “e” occurs more often than “a,” and “a” occurs more often than “g,” which in turn occurs more often than “x.” Put it all together and it looks something like this:

So now imagine we put all our letters (and a space) in a hat. But instead of 1 letter each, we have 100 total tiles in the hat and they align with the chart above: 13 tiles for “e”, 4 tiles for “d”, 1 tile for “v”. Here’s what Shannon got when he did this:

OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL

He called this “first-order approximation” and while it still doesn’t make much sense, it’s a lot less random than the first example.

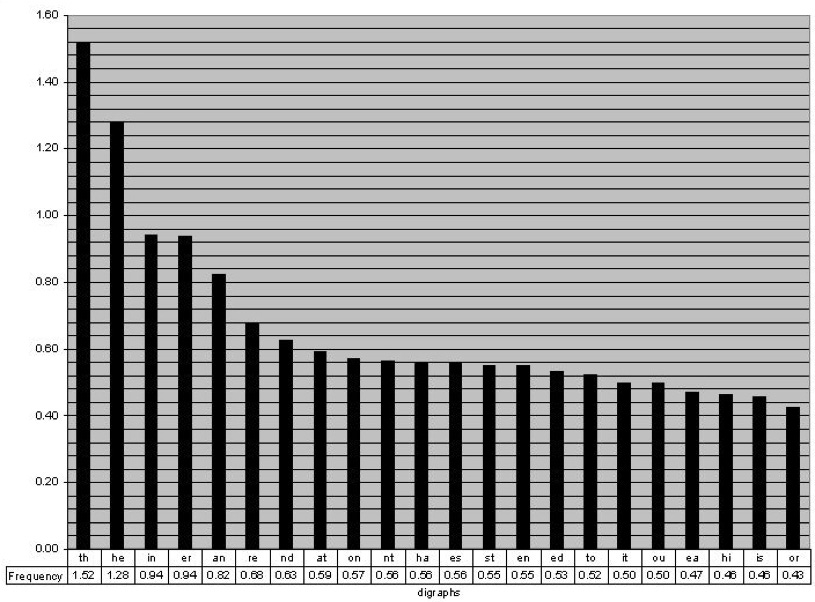
What’s wrong with that last example is that letters don’t operate independently. Let’s play a game for a second. I’m going to say a letter and you guess the next one. If I say “T” the odds are most of you are going to say “H”. That makes lots of sense since “the” is the most popular word in the English language. So instead of just picking letters at random based on probability what Shannon did next is pick one letter and then match it with its probabilistic pair. These are called bigrams and just like we had letter frequencies, we can chart these out.

This time Shannon took a slightly different approach. Rather than loading up a bunch of bigrams in a hat and picking them out at random he turned to a random page in a book and choose a random letter. He then turned to another random page in the same book and found the first occurrence of recorded the letter immediately after it. What came out starts to look a lot more like English:

ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE

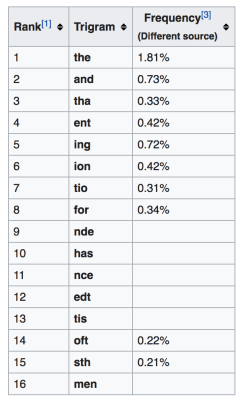
Now I’m guessing you’re starting to see the pattern here. Next Shannon looked at trigrams, sets of three letters.

For his “third-order approximation” he once again uses the book but goes three letters deep:

IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE

He could go on and on and it would become closer and closer to English. Instead, he switches to words, which also occur probabilistically.

For his “first-order approximation” he picks random words from the book. It looks a lot like a sentence because words don’t occur randomly. There’s a good chance an “and” will come after a word because “and” is likely the third most popular word in the book. Here’s what came out:

REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE.

Second-order approximation works just like bigrams, but instead of letters, it uses pairs of words.

THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.

As Shannon put it, “The resemblance to ordinary English text increases quite noticeably at each of the above steps.”

While all that’s cool, much of it was pretty well known at the time. Shannon had worked on cryptography during World War II and used many of these ideas to encrypt/decrypt messages. Where the leap came was how he used this to think about the quantity of information any message contains. He basically realized that the first example, with 27 random symbols (A-Z plus a space), carried with it much more information than his second- or third-order approximation, where subsequent letters were chosen based on their probabilities. That’s because there are fewer “choices” to be made as we introduce bigrams and trigrams, and “choices”, or lack thereof, are the essence of information.

It’s one of those ideas that takes a while to fully get (I highly suggest this excellent Khan Academy video if you need another pass) but once understood, it totally reshapes how you understand the world. Art’s appeal, at least in part, is likely due to unpredictability—there’s a lot of information. Buzzwords, on the other hand, are so frustrating because of just how predictable, and therefore information-less, they eventually become. Without information theory, we wouldn’t have computers or phones or any of the trappings that come along with them. But more fundamentally, we would have a far more incomplete understanding of how our world works. (NRB)

Chalk of the Day:

I loved this Twitter thread on Hagoromo Fulltouch chalk, which is apparently the most sought-after chalk amongst mathematicians. (Thanks to SV4 for the tip.) (NRB)

Quick Links:

• We were promised Strong AI, but instead, we got metadata analysis (NRB)

• Fly fishers hit out at Supreme’s ‘laughable’ range of utility wear (NRB)

• In Punishing Russia for SolarWinds, Biden Upends U.S. Convention on Cyber Espionage (NRB)

Thanks for reading,

Noah (NRB) & Colin (CJN)

—

Why is this interesting? is a daily email from Noah Brier & Colin Nagy (and friends!) about interesting things. If you’ve enjoyed this edition, please consider forwarding it to a friend. If you’re reading it for the first time, consider subscribing (it’s free!).