The P vs. NP Edition
On complexity, computer science, and time
Subscribe to WITI for $7 a month:
Noah here. A few years ago, I went deep into a physics and math rabbit hole. I can’t remember if it started with books or YouTube lectures, but what began as an interest in understanding some scientific basics like E=mc^2, cascaded into reading about quantum mechanics and the Poincaré Conjecture. There was some real magic in trying to wrap my head around seemingly impossible concepts, and I came to appreciate (to whatever extent a layperson like myself can) how mind-bending it must be to work as a theoretical physicist or mathematician.
Over the last few weeks, I’ve been returning to the rabbit hole a bit as I make my way through the backlog of Caltech physicist Sean Carrol’s Mindscape podcast. Carrol turns out to be quite an adept interviewer, as he deeply understands the topics his guests are discussing but maintains both the curiosity and self-control to allow them to speak, only occasionally jumping in to clarify.
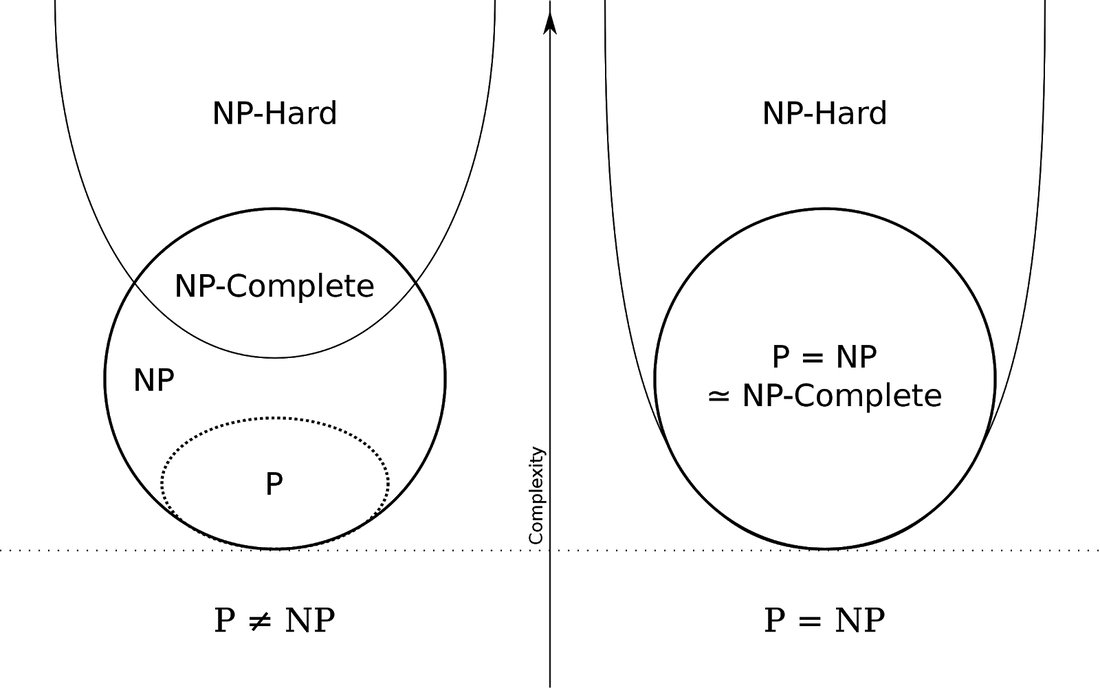
One recent episode I listened to was with theoretical computer scientist Scott Aaronson. I wrote about Aaronson a bit last year as quantum supremacy made the news, but for this conversation, he was more focused on a concept called complexity classes, and the computer science (CS)/math problem P vs. NP. P vs. NP is one of the great unsolved problems in cs/math and is one of the seven Clay Institute Millenium Problems with a million-dollar bounty. To get that million, all you have to do is prove that there’s a difference (or not) between problems that are easy for computers to solve (P) and those that are hard (NP). If that sounds a little crazy, it’s because it is. Nearly every person working on P vs. NP believes that P is not the same as NP—that there is some fundamental distinction between what is easy and hard for a computer to solve—but to this point, no one has proven this is true.
Why is this interesting?
Easy and hard are shorthand for how computer scientists talk about computational complexity. To those in CS, complexity is a way to articulate how difficult a particular computation is to solve, as measured by the time or memory required to process it. Most things we ask a computer to do are relatively straightforward: sorting a list of words alphabetically, for example, can happen nearly instantaneously even if that list is 20,000 words long. These are called “P” problems because a regular computer can solve them in polynomial time. Polynomial-time is most easily understood as the number of elements you’re processing—say words in a list that need to be sorted—raised to a fixed power like n^2 or n^5 (Substack doesn’t support exponents, sorry about the weird notation). The thing to understand about P problems is that even if one took n^100 time, a computer scientist would still consider it “easy” to solve because the exponent is fixed. Easy, in other words, doesn’t always mean fast.
Consider the problem of sorting a list. Even if we’re sorting a billion items, we have algorithms that allow us to find the answer without trying out every permutation. Bubble sort, for instance, goes through a list of numbers and switches the position of any two neighbors to put them in the right order. After it finishes a pass, it goes through a second, third, fourth, and so on, until the list is finally in the correct order and requires no more switching. (The GIF below, taken from Wikipedia, is an excellent primer.)
As you likely noticed, bubble sort is not a particularly efficient way of ordering something. Still, it gets the job done faster than laying out all the possible combinations of numbers until you find the one that happens to be in the right order. As a result, it counts as “easy,” despite its relative inefficiency. In a massively over-simplistic sense, you can think of P problems as anything for which we have a better approach than trial-and-error for solving them.
Bubble sort visualized in static form
On the other hand, some problems are more challenging for computers to solve: cryptographic techniques like finding prime factors, playing games like sudoku, solving math/logic questions like the traveling salesman problem, and even finding the right configuration of packing boxes in your trunk, are all “hard” in CS terms. In other words, we don’t have an efficient algorithm to solve them. In the case of sudoku, while it might be easy to do the puzzle in your Sunday paper, imagine trying to solve a billion square grid. The good news is that no matter how many years or lifetimes it took to complete the puzzle, once you were done, checking it was all correct would be nearly effortless for your computer. Sudoku and the like are “NP” problems, which annoyingly doesn’t mean “not polynomial,” and instead stands for non-deterministic polynomial time. What unites these problems is that no computer we have ever built can solve them in polynomial time. In fact, many of them take an exponential amount of time to figure out—so instead of n^2 (polynomial) time, they might take 2^n (exponential) time, which, if you remember back to high school math, means they can get big fast. However, as in the sudoku example, once any NP problem is solved, checking it’s correct is a breeze.
The debate of P vs. NP, which may sound ridiculous, is whether the two classes are actually different. Are NP problems just P problems for which we haven’t discovered a better algorithm? While almost every mathematician and computer scientist believes the P≠NP, they haven’t been able to prove that there’s something fundamentally different about the problem posed by sudoku versus sorting a list of letters alphabetically. On the one hand, as I said earlier, this is crazy. If there turned out to indeed be no difference between these classes of problems, many of the unsolved math problems in the world would disappear. There’s actually a whole class of problems called NP-complete that, if any one of them were solved, would unlock all the others.
If P were equal to NP, there would still be unanswered questions in the universe, but in mathematics, at least, we’d be able to point powerful computers at many of them, and they’d fall away. This seems so obviously impossible that it’s kind of amazing to imagine some of the smartest people on our planet being willing to entertain it. But I guess that’s what you do if you’re a theoretical computer scientist. Or if you just need an escape from the news. (NRB)
WITI x McKinsey:
An ongoing partnership where we highlight interesting McKinsey research, writing, and data.
When will the COVID-19 pandemic end? The Omicron variant is spreading rapidly; what does it mean? Our modeling offers some scenarios to understand potential outcomes. We also cover three other new developments on the bumpy road to endemicity. Navigate new developments here.
Thanks for reading,
Noah (NRB) & Colin (CJN)
—
Why is this interesting? is a daily email from Noah Brier & Colin Nagy (and friends!) about interesting things. If you’ve enjoyed this edition, please consider forwarding it to a friend. If you’re reading it for the first time, consider subscribing (it’s free!).