Why is this interesting? - The Airplane Boarding Edition
On queuing, bottlenecks, and the theory of constraints
Noah here.Anyone who has ever boarded a plane has surely thought to themselves “this can’t be the best way to do this.” Whether it’s front-to-back, back-to-front, windows first, or the increasingly popular “group numbers”, the method seems to lead to frustration for everyone involved. When we overlay the increasingly complicated boarding rules brought by loyalty and credit card incentives, in addition to additional bag check fees leading to more people cramming their belongings in the overhead bin, this angst is further exacerbated.
If you’re an astrophysicist that frustration leads you to spend some time trying to find a more optimal method. His big discovery is that it's the people loading luggage causing bottlenecks: “The model that I employ assumes that the time that a passenger requires to load his or her luggage is the dominant contribution to the time needed to completely fill the aircraft. The optimal boarding strategy may reduce the time required to board and [sic] airplane by over a factor of four and possibly more depending upon the dimensions of the aircraft.”
So what would work better than our current approach? Just about anything. As CNET reported, “He found that the most efficient boarding method is to board alternate rows at a time, beginning with the window seats on one side, then the other, minimizing aisle interference. The window seats are followed by alternate rows of middle seats, then aisle seats. He also found that boarding at random is faster than boarding by blocks.” Random!
Why is this interesting?
This type of problem-solving is called queuing theory and is used heavily in operations. After all, what is a manufacturing chain other than a long queue of things to be done? What’s fascinating about it, though, is how surprising some of the results can be. Take this example of bank tellers, for instance:
Suppose a small bank has only one teller. Customers take an average of 10 minutes to serve and they arrive at the rate of 5.8 per hour. What will the expected waiting time be? What happens if you add another teller?
We assume customer arrivals and customer service times are random (details later). With only one teller, customers will have to wait nearly five hours on average before they are served. But if you add a second teller, the average waiting time is not just cut in half; it goes down to about 3 minutes. The waiting time is reduced by a factor of 93x.
Why was the wait so long with one teller? There’s not much slack in the system. Customers are arriving every 10.3 minutes on average and are taking 10 minutes to serve on average. If customer arrivals were exactly evenly spaced and each took exactly 10 minutes to serve, there would be no problem. Each customer would be served before the next arrived. No waiting.
In the end, all this stuff comes down to finding bottlenecks: The parts of the process that limit the speed of everything that happens after it. The best book I know of on bottlenecks is the cheesy but excellent The Goal by Eliyahu Goldratt (also available—and recommended—in graphic novel form). The book revolves around Goldratt’s “theory of constraints” and the five focusing steps to uncover bottlenecks, which I’ve found to be a helpful framework to apply to almost any process (his weird words are followed by my simplified explanation):
Identify the system’s constraint: Figure out where your bottleneck is
Decide how to exploit the system’s constraint: Optimize the bottleneck as much as you can
Subordinate everything else to the above decision: Since everything is subject to the bottleneck, you want to make sure you reorient things to work with, not against your bottleneck
Elevate the system’s constraint: Basically, if you’ve done the first three well, you should now be able to run more through the process
Go back to step 1. Do not allow inertia to cause a system’s constraint: Rinse and repeat.
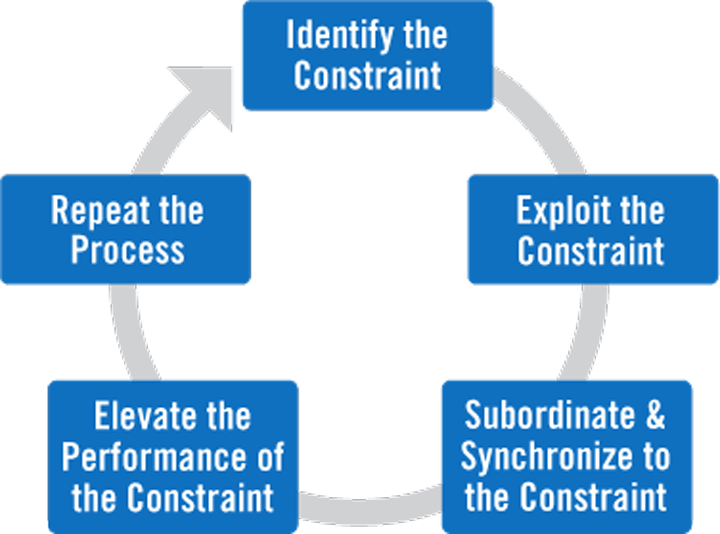
Obviously, queuing theory is a much more mathematical approach to the problem, but in the end, it’s all about trying to figure out what’s limiting throughput and finding alternative approaches to solving the problem. (NRB)
Chart of the Day:
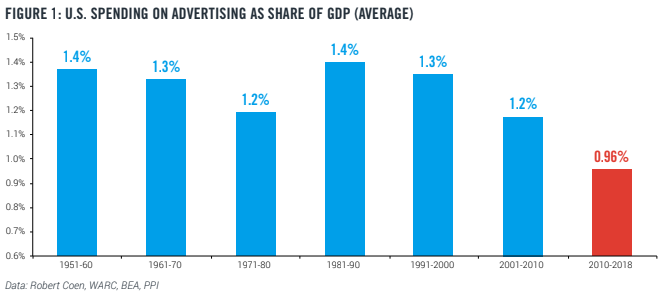
Ad spend has historically tracked pretty closely to GDP. Are we seeing that split for the first time? [Via @BluegrassCap] (NRB)
Quick Links:
This is definitely my experience: 'Free Solo' Is Secretly a Classic Horror Movie [via BP] (NRB)
This was a cool episode of the journal Nature’s podcast: “In the early 1990s, a team of astrophysicists led by Carl Sagan looked at data from the Galileo spacecraft and saw the signatures of life on a planet in our galaxy. Historian of science David Kaiser and astrobiologists Charles Cockell and Frank Drake discuss how we can tell if there is life beyond the Earth – and how optimism, as well as science, is necessary for such a venture.” (NRB)
I was reminded of this excellent 1992 William Finnegan New Yorker piece on surfing that he eventually turned into the Pulitzer Prize-winning Barbarian Days. (NRB)
Thanks for reading,
Noah (NRB) & Colin (CJN)
PS - Noah here. I’ve started a new company and we are looking for a sr. backend engineer to join the team. If you are one of those or know anyone who is great, please share. Dinner’s on me at a restaurant of your choice if you help us find someone.
Why is this interesting? is a daily email from Noah Brier & Colin Nagy (and friends!) about interesting things. If you’ve enjoyed this edition, please consider forwarding it to a friend. If you’re reading it for the first time, consider subscribing (it’s free!).


