Why is this interesting? - The Pythagorean Edition
On triangles, heaven, and simultaneous discovery
If you are curious why this WITI arrived in the evening, it’s a regular story of trying to do two things at once (in this case, queue an e-mail and walk the dog) and I hit the wrong button. We will be back to our regular schedule Monday morning. - Noah
Steve Bryant (SB) is a content strategy consultant, co-founder of the midnight costumed adventure Rental Car Rally, founding editor of InsideHook, and a longtime friend of WITI (he wrote our very first guest edition on Maslow).
Steve here. Discoveries are often made by multiple people, but we tend to only remember one of those folks. This is just as true for the theory of evolution (Wallace, but also Darwin), as it is for lightning rods (Diviš, but also Franklin), as it is for the electrical telegraph—invented by Wheatstone but also Morse, whose first message is a favorite of trivianauts and bibliophiles alike (“what hath god wrought”, Numbers 23:23).
The concept of multiple discovery also happens to apply to a favorite hobbyhorse of mine, the Pythagorean Theorem—the formula that allows you to deduce the area of a square alongside a triangle’s hypotenuse, which in turn allows you to develop trigonometry, which in turn allows you to (eventually) navigate the ocean using a sextant and (even further eventually) calculate things like the height of Mount Everest without climbing it and the fastest route via Google Maps.
Now any Tom, Dick, or Platonist can tell you that the Pythagorean Theorem was first set down as an axiomatic proof in Euclid’s Elements around 300BCE. It is slightly less well known (tho very Wikipediable) that parts of the theorem were known as early as 3000 BCE as far away as India and China. As with all multiple discoveries, the interesting question is...how? How did multiple people discover the same thing? And in this case, given that the theorem empirically describes geometric reality, was there any similarity in the thought process that led people thousands of miles distant and thousands of years apart to discover it? I mean, everyone was just trying to create, like, wagon wheels...right?
Hoo boy, not at all! The triangles in Babylon are the triangles in Punjab are the triangles in Fenghao, but the reason for developing those triangles was wildly different.
Why is this interesting?
Those differences reveal quite a lot about how different cultures pursued knowledge, and even how they valued the practice of learning. My favorite example comes by way of an ancient Chinese concept called the Mandate of Heaven.
Popularized by the Zhou Dynasty beginning around 1100 BC, the Mandate of Heaven argued that heaven, not blood, grants the emperor the right to rule. Heaven, the argument went, decides whether a ruler is “virtuous”, and that virtue allows him or her to rule.
This, as you might imagine, was a BHD (Big Historical Deal). By doing away with rule by royalty, the mandate opened leadership to the people and justified rule by rebellion and force (“I have the mandate, follow me!”). By tying leadership to virtue, the mandate also required rulers to be responsible (“I treat you well, keep following me!”). But by leaving “virtue” open to interpretation, the mandate incentivized rulers to, well, make shit up. In practice, it meant that rulers had to secure the mandate through tangible and explicable communications with heaven, and explain every chance event (comets, earthquakes, famine, etc) as a positive sign of heaven’s unwavering aegis.
As you might imagine, trying to convince people at every moment that heaven loves the emperor can be ≋c≋r≋a≋z≋y≋ ≋m≋a≋k≋i≋n≋g≋. Rulers had to make sacrifices on mountain tops and create calendars to predict celestial events and build temples to receive heaven’s blessing. In other words, they had to enact the reality they wished their followers to believe in. It was there, in the midst of all that performative interpretation, that the triangles come in.
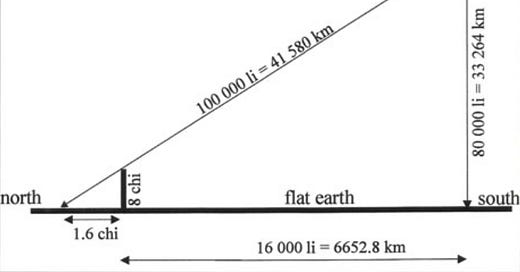
The Chinese of the first millennium BCE believed Earth was a square and heaven was a circle. As in: the Earth was a flat, four-cornered thing, and heaven existed as a flat disc directly above it. The sun, according to this conception, was 80,000 li away (roughly 20,790 miles):
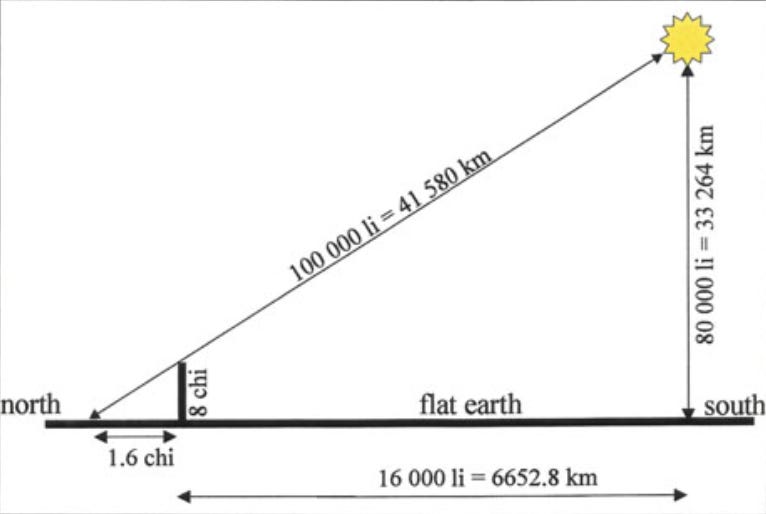
To make this concept understandable, they likened the square to a chariot. They likened the circle to the canopy that stood above that chariot. They called this concept “Canopy Heaven”.

Over time, Canopy Heaven fell out of favor. If Heaven were exactly round and Earth exactly square and both were exactly the same size then that meant, some argued, that the four angles of square Earth would not be well-covered by circular heaven.
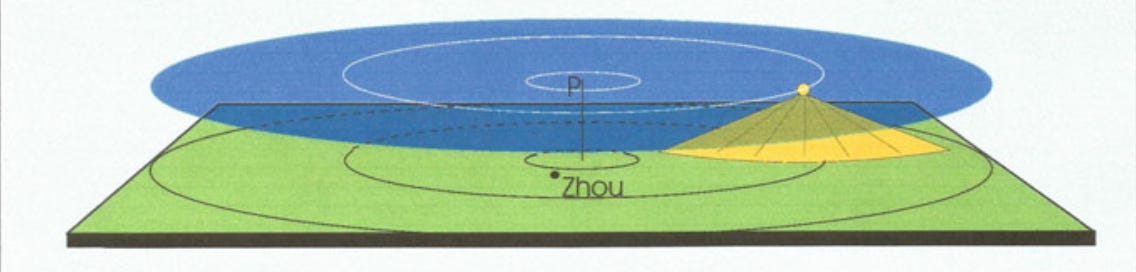
Owing to this lack of figurative accuracy, the concept of Canopy Heaven began to be replaced by another concept—Spherical Heaven—whose main assumption was that Heaven contains Earth in the same way that an egg contains the yolk. Clearly, more rigorous minds had prevailed.
But some mathematicians couldn’t let the idea of Canopy Heaven go. The author of the Zhou Gnomon, a mathematical classic compiled in the first century BCE, turned the problem of joining a round Heaven and a square Earth into the problem of arranging a circle and a square on a plane, especially one within the other. From that attempt to reason out the physical connection between the circle of Heaven and the square of Earth, some historians argue, the author deduced an instance of the Pythagorean Theorem.
So to sum up: The ancient Chinese derived a geometric truth because they believed they had to keep despots off the throne, and in order to keep despots off the throne they had to maintain heaven’s favor, and in order to maintain heaven’s favor they had to prove the earth was shaped like a square and that heaven was shaped like a circle directly above it. Which is to say that even the most enthusiastically wrongheaded folks can, in the attempt to justify their own moral superiority, make some useful discoveries—it’s just a long way to go for a ham sandwich.
That would be the end of our story but, to bring this argument to a π-like full circle, it’s important to note a few important contextual bits and bobs. While the ancient Chinese did develop geometric principles, and they did develop those principles in pursuit of judging heaven’s height, there is debate about whether their mathematicians used “proofs”. This may seem like a minor point, but the debate suggests that Chinese mathematicians couldn’t “discover” the Pythagorean Theorem if they didn’t “show their work” in the same way the Greeks did.
But that equivalency suggests a biased reasoning. Perhaps looking for a Chinese equivalent to Grecian methodology is, itself, an ethnocentric expectation. As some historians have noted, giving a Euclid-like proof wasn’t as important to Chinese mathematicians as explaining the use of the methods they were expounding to solve certain problems. It’s only the Western value system, which was written into the history books during the 18th century’s so-called opening of China, that argues for the supremacy of the Grecian way of thinking.
This debate about ancient geometry extends like a straight line into infinity, and it’s beyond the scope of this piece to address it all. Suffice to say that the Pythagorean Theorem was discovered, in one way or another, and for one reason or another, several times by several different people on several different continents. Some of those people cared about the heights of heaven. Others cared about the heights of philosophy. There’s an elegant equivalence there, if you do the math.
And anyway no matter where you are, like Euclid said, all right angles are equal to each other. (SB)
Books of the Day:
I am neither a historian or an expert in Chinese history, and to write this piece I relied on significant portions of the following books. I especially recommend Cullen for his rigorous analysis of mathematical artifacts, Tseng for her great overview of ancient theology, and Chemla et al for their inclusive approach to historical maths. (SB)
Karine Chemla, The History of Mathematical Proof in Ancient Traditions, (Cambridge University Press, 2012)
Dirk L. Couprie, When the Earth was Flat: Studies in Ancient Greek and Chinese Cosmology, (Springer Nature Switzerland, 2018)
Christopher Cullen, Astronomy and Mathematics in Ancient China (New York: Cambridge University Press, 2007)
Michael Loewe, Edward L. Shaughnessy, The Cambridge History of Ancient China: From the Origins of Civilization to 221 BC (Cambridge University Press, 1999)
Lillian Lan-ying Tseng, Picturing Heaven in Early China (New York: Harvard University Asia Center, 2011)
Quick Links:
The Cold War Bunker That Became Home to a Dark-Web Empire (NRB)
Cloudflare has a really nice speed test page (something I’m doing a lot more of these days) (NRB)
Thanks for reading,
Noah (NRB) & Colin (CJN) & Steve (SB)
PS - Noah here. Variance, my new company, is just getting going with our Alpha. If you work in sales, services, marketing, or engineering and want to try out/give feedback on a tool to help your team work more effectively with their apps, please request an invite on the site. Thanks.
—
Why is this interesting? is a daily email from Noah Brier & Colin Nagy (and friends!) about interesting things. If you’ve enjoyed this edition, please consider forwarding it to a friend. If you’re reading it for the first time, consider subscribing (it’s free!).