Why is this interesting? - The Volatility Edition
On finance, physics, and the models we use to understand the world
Emanuel Derman (ED) wrote the excellent Being Foreign, Japan, and E Pluribus Unum Editions. He grew up in Cape Town, South Africa, and came to Columbia University in New York to study for a PhD in physics. Since then he’s lived mostly in Manhattan. His memoir is My Life As A Quant. - Colin (CJN)
Emanuel here. Volatility is the propensity to continually change one’s current state, irrespective of the direction of the change. You could argue that the elimination of volatility is the implicit (perhaps futile) aim of Economic and Political Science, and that the toleration of volatility is the aim of psychotherapy.
In physics, a volatile liquid easily undergoes a phase transition into a gas. Volatile substances can sublimate, moving directly from solid to vapor. (“Everything solid melts into air,” as Marx and Engels wrote about modernity.) In humans, volatility characterizes an easy excitability that moves swiftly from calmness to agitation and back again.
Volatility involves uncertain changes of state. In physics one can go a long way before having to theorize about uncertainty. The great founding triumphs of theoretical prediction, from Kepler to Newton, ignored uncertainty. In the late 1800s Gibbs, Maxwell, and Helmholtz explained the behavior of gases by regarding them as statistical averages over the random distributions of their microscopic atoms whose speeds and positions just happened to be unknown but not unknowable. In 20th Century quantum mechanics, however, uncertainty became intrinsic rather than accidental. Unknowability is baked in, puzzlingly undodgeable.
Why is this interesting?
Whereas uncertainty came late in the discussion of matter, it was there right at the start of finance. When you buy a stock, you cannot know what return you will have earned in the future. Time and chance happen to us all. A stock price that moves unpredictably up and down is volatile. Its volatility reflects the unstable equilibrium between two simultaneous but conflicting occurrences: good news and bad news, the desire to buy and the desire to sell, in permanent conflict. As in politics, there is no volatility without conflict.
Stock prices are not concrete in the way that atoms are; they are more mental than physical. The struggle to comprehend their volatility has devolved around how to quantify the fluctuating nature of prices, affected, of course, by the fluctuating nature of the world and the fluctuations of human feelings. It has become traditional to model the uncertain nature of mental stock prices by analogy with the random movement of physical atoms. More about this at the end.
Gases diffuse through space as their atoms sometimes get jolted left and sometimes right by other atoms. Adolf Fick in 1855 derived the diffusion equation, a partial differential equation that describes the diffusion quantitatively. Since the 1960s financial theorists have described the behavior of stock prices analogously. As pictured crudely below, a stock whose initial price is 100 has equal probabilities of being jostled up or down by a small amount, here 1%, in the next very short instant of time δt.

This is what it looks like after six successive instants have passed.

The numbers on the right-hand side indicate the possible stock prices. The red line represents their probability. You can see the volatility.
After this happens repeatedly, many many times, the stock price in this model is eventually distributed according to a normal or Gaussian distribution. In Germany where they honor scientists and artists rather than only politicians, you could find Gauss and his distribution (like the red line above) pictured on the old 10-Mark note. The famous Black-Scholes model for options prices is based on a version of the diffusion equation applied to mental things (stock prices) rather than physical things (gases).

Under the originally plausible notion that this approach captures reality, it seemed possible that one could buy and sell stock market volatility. At times, this can be done. But, if you’ve been watching the market during the pandemic, you will have observed that stocks don’t always go up or down by a small amount of 1% or less. Sometimes they jump down (more often) and up (less often) by a giant amount, say 10% or even 20% during a day.
The evolution of stock prices that can jump an arbitrary amount at any time in the future leads to what is colloquially called a fat-tailed distribution, because its tail—the likelihood of making a big up or down move—is much greater than that of a Gaussian distribution. The figure below shows the distribution of 2000 daily returns for Apple stock, compared to a Gaussian. You can see the small but significant fat tails, especially on the left side. Persisting in the use of Gaussian distributions, as emphasized by Nassim Taleb, sweeps under the rug much of the danger of owning stocks.
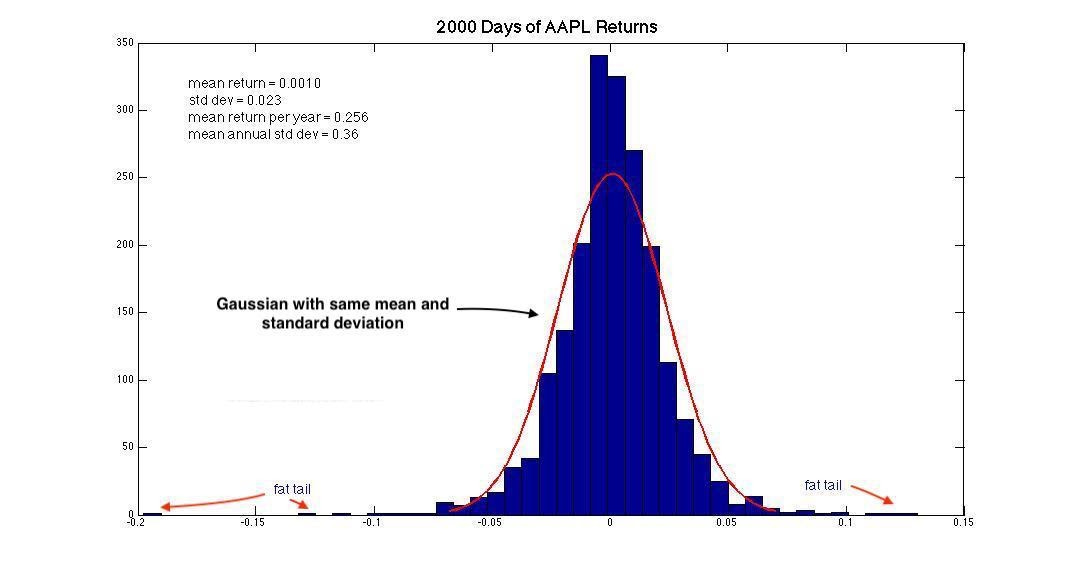
Most financial models, even ones that try go beyond the Gaussian, use the behavior of physical things as a metaphor for the behavior of mental things. But we always understand the rules of the physical better than the rules of the mental, and so we still struggle. (ED)
Image of the Day:
From the European Southern Observatory: “This image shows the disc around the young AB Aurigae star, where ESO’s Very Large Telescope (VLT) has spotted signs of planet birth. Close to the centre of the image, in the inner region of the disc, we see the ‘twist’ (in very bright yellow) that scientists believe marks the spot where a planet is forming. This twist lies at about the same distance from the AB Aurigae star as Neptune from the Sun.” (NRB)

Quick Links:
What's supercharging Amphan? (NRB)
Do rehabs actually work? (NRB)
Very cool Quanta timeline of our understanding of time (NRB)
Thanks for reading,
Noah (NRB) & Colin (CJN) & Emanuel (ED)
—
Why is this interesting? is a daily email from Noah Brier & Colin Nagy (and friends!) about interesting things. If you’ve enjoyed this edition, please consider forwarding it to a friend. If you’re reading it for the first time, consider subscribing (it’s free!).
